영상 처리에서는 처리 공간은 크게 공간영역, 주파수 영역이있습니다.
이번 시간에는 주파수 영역에서 처리하기 위해 이미지를 주파수 영역으로 변환 시키고 시각화 해보는 것을 진행해 보겠습니다.
이미지는 디지털 영상으로 디지털 신호로 구분됩니다. 따라서 주파수 도메인으로 변경을 위해 주로 DCT를 사용합니다.
하지만 저는 DCT를 사용할 계획입니다.
DCT
DCT는 FT(Fourrier Transform)의 변형으로 cosine 성분만을 가지고 변환을 진행합니다. 기존의 DFT는 sine과 cosine 정현파로 구분했지만 sine성분의 크기가 무시해도 될 정도로 작으며 연산의 복잡도를 감소 시키기 위해 cosine 성분만 사용한 FT를 적용합니다.
왜 주파수 영역에서 처리를 하느냐?
신호 처리과정은 주파수 영역에서 해석이 유리해 집니다. 이미지 신호는 신호값을 x,y 위치변수에 따른 픽셀 값으로 볼 수 있습니다. 따라서 주파수는 pixel의 변화량 이라고 볼 수 있고 변화량이 큰 곳을 "고주파", 변화량이 작은 곳은 "저주파"로 볼 수 있습니다. 우리가 접하는 모든 영상들이 고주파 성분보다 저주파 성분을 훨씬 많이 포함하고 있기 때문에 이러한 변환을 이용하여 주파수 성분으로 영상을 분할한 뒤 파일 압축에 사용할 수 있습니다.
( 영상처리를 진행 할 때 Lenna 사진을 사용한 이유가 고주파 성분과 저주파 성분이 적절하게 배치되어서 라고 합니다. )
DCT 공식은 다음과 같습니다.

전체 영상에 걸쳐 위의 연산을 처리하기에는 엄청난 연산 비용이 사용됩니다.
그래서 영상처리에서는 주로 DCT를 8 x 8 Block 단위로 사용합니다. 실제로 Block의 크기는 고정되지 않앟지만 가장 많이 사용되는 크기가 8 x 8 입니다.
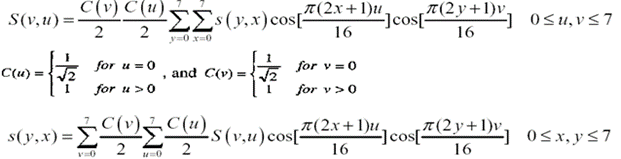
영상의 효율적인 압축을 위해서 양자화를 진행합니다. 이 과정은 고주파에 둔감하고 저주파에 민감한 인간의 눈의 특성을 고려하여 고주파 성분을 0에 가까운 값으로 만들어서 압축효과를 얻기 위함입니다.
(고주파는 이미 픽셀 변화가 많기 때문에 변화가 있어도 둔감하게 느껴질 수 있습니다. )
아래 표는 양자화를 위한 숫자입니다. 8 x 8 단위의 Block단위의 DCT가 완료된 후 Block의 위치별로 1:1로 나누어 주고 Inverse 과정에서는 1:1로 곱해주게 됩니다.

코드 실습
FDCT , IDCT 과정을 코드로 실습하겠습니다.
8x8 단위, 8x8 단위 + 양좌화 , 영상 전체에 걸친 DCT 3가지에 대해서 실습했습니다.
double C(int v) {
if (v == 0) {
return double(1) / sqrt(2);
}
else {
return 1;
}
}
void i_dct(int y_start, int x_start, unsigned char** output) {
int i, j, v, u;
double sum = 0;
for (j = 0; j < 8; j++) {
for (i = 0; i < 8; i++) {
for (v = 0; v < 8; v++) {
for (u = 0; u < 8; u++) {
sum += (temp[y_start + v][x_start + u] * cos(M_PI * (2 * i + 1) * u / 16.0)
* cos(M_PI * (2 * j + 1) * v / 16.0) * C(u)* C(v));
}
}
sum /= 4.0;
if (sum > 255) sum = 255;
if (sum < 0) sum = 0;
output[y_start + j][x_start + i] = sum;
sum = 0;
}
}
}
void dct(int y_start, int x_start, unsigned char** input,unsigned char** output) {
double sum = 0;
for (int v = 0; v < 8; v++) {
for (int u = 0; u < 8; u++) {
for (int j = 0; j < 8; j++) {
for (int i = 0; i < 8; i++) {
sum += (double)input[y_start + j][x_start + i] * (double)cos(M_PI * (2 * i + 1) * u / 16.0) * (double)cos(M_PI * (2 * j + 1) * v / 16.0);
}
}
temp[y_start + v][x_start + u] = C(v) * C(u) / 4.0 * sum;
output[y_start + v][x_start + u] = C(v) * C(u) / 4.0 * sum;
if (C(v) * C(u) / 4.0 * sum > 255) {
output[y_start + v][x_start + u] = 255;
}
if (C(v) * C(u) / 4.0 * sum < 0) {
output[y_start + v][x_start + u] = 0;
}
sum = 0;
}
}
}8x8 block를 활용한 DCT 입니다.
unsigned char matrix[8][8] = { {16,11,10,16,24,40,51,61},
{12,12,14,19,26,58,60,55},
{14,13,16,24,40,57,69,56},
{14,17,22,29,51,87,80,62},
{18,22,37,56,68,109,103,77},
{24,35,55,64,81,104,113,92},
{49,64,78,87,103,121,120,101},
{72,82,95,98,112,100,103,99}
};Quantization(양자화)를 위한 matrix를 생성해 주고 Mask 연산을 진행해 줍니다.
void f_dct(unsigned char** input) {
double sum = 0;
for (int u = 0; u < VER; u++) {
for (int y = 0; y < VER; y++) {
for (int x = 0; x < VER; x++) {
sum += input[y][x] * cos(M_PI * (2 * x + 1) * u / (2 * 512));
}
x_cos[u][y] = sum;
x_cos[u][y] = x_cos[u][y] * C(u) / 16.0;
sum = 0;
}
}
for (int v = 0; v < VER; v++) {
for (int u = 0; u < VER; u++) {
for (int y = 0; y < VER; y++) {
sum += cos(M_PI * (2 * y + 1) * v / (2 * 512)) * x_cos[u][y];
}
sum = sum * C(v) / 16.0;
transf[v][u] = sum;
sum = 0;
}
}
}
void i_f_dct(unsigned char** output) {
double sum = 0;
for (int x = 0; x < VER; x++) {
for (int v = 0; v < VER; v++) {
for (int u = 0; u < VER; u++) {
sum += transf[v][u] * cos(M_PI * (2 * x + 1) * u / (2 * 512))*(C(u)/16.0);
}
x_cos[x][v] = sum;
sum = 0;
}
}
for (int y = 0; y < VER; y++) {
for (int x = 0; x < VER; x++) {
for (int v = 0; v < VER; v++) {
sum += cos(M_PI * (2 * y + 1) * v / (2 * 512)) * (C(v) / 16.0) * x_cos[x][v];
}
if (sum > 255) sum = 255;
if (sum < 0) sum = 0;
output[y][x] = sum;
sum = 0;
}
}
}
영상 전체의 걸친 DCT 과정입니다. 다만 여기서 주의할 점은 위 수식을 통해 3중 for문으로 구현하게 되면 512x512 이미지에 대해서 진행하는데 8시간 정도가 걸린다. 다라서 2중 for문 2개로 바꿔서 진행해 줘야한다.
결과

위의 DCT를 수행한 후 결과를 보면 영상의 대부분이 검정색임을 볼 수있는데, 이렇게 검정색이 많은 영상들이 Inverse DCT를 거친 후 복원된 결과를 보면 눈으로 구분하기엔 원본과 차이가 없음을 알 수 있다. 이것이 DCT를 사용하는 가장 큰 이유이다.



